Pokud je vaším cílem použít profilovač, použijte jeden z navrhovaných.
Pokud však spěcháte a můžete ručně přerušit svůj program pod debuggerem, zatímco je subjektivně pomalý, existuje jednoduchý způsob, jak najít problémy s výkonem.
Stačí to několikrát zastavit a pokaždé se podívat na zásobník hovorů. Pokud existuje nějaký kód, který plýtvá nějaké procento času, 20% nebo 50% nebo cokoliv jiného, je to pravděpodobnost, že ho chytíte při činu na každém vzorku. To je tedy zhruba procento vzorků, na kterých to uvidíte. Není třeba žádného vzdělaného odhadu. Pokud máte tušení, v čem je problém, toto to potvrdí nebo vyvrátí.
Můžete mít více problémů s výkonem různých velikostí. Pokud některý z nich vyčistíte, zbývající budou mít větší procento a budou snadněji rozpoznatelné při dalších průchodech. Tento efekt zvětšení , když se spojí s více problémy, může vést ke skutečně masivním faktorům zrychlení.
Upozornění :Programátoři mají tendenci být k této technice skeptičtí, pokud ji sami nepoužili. Řeknou, že vám tyto informace poskytnou profilovači, ale to je pravda pouze tehdy, když vzorkují celý zásobník hovorů a pak vás nechají prozkoumat náhodnou sadu vzorků. (V souhrnech se ztrácí přehled.) Grafy hovorů neposkytují stejné informace, protože
- Neshrnují na úrovni pokynů a
- Za přítomnosti rekurze poskytují matoucí souhrny.
Také řeknou, že to funguje pouze na hracích programech, i když to ve skutečnosti funguje na jakémkoli programu, a zdá se, že to funguje lépe na větších programech, protože mají tendenci mít více problémů s hledáním. Řeknou, že někdy najde věci, které nejsou problémové, ale to je pravda pouze tehdy, když něco uvidíte jednou . Pokud vidíte problém na více než jednom vzorku, je to skutečné.
P.S. To lze také provést u programů s více vlákny, pokud existuje způsob, jak shromáždit vzorky zásobníků volání fondu vláken v určitém okamžiku, jako je tomu v Javě.
P.P.S Zhruba obecně řečeno, čím více vrstev abstrakce ve svém softwaru máte, tím pravděpodobněji zjistíte, že to je příčinou problémů s výkonem (a příležitostí ke zrychlení).
Přidáno :Nemusí to být zřejmé, ale technika vzorkování zásobníku funguje stejně dobře i v přítomnosti rekurze. Důvodem je, že čas, který by se ušetřil odstraněním instrukce, je aproximován zlomkem vzorků, které ji obsahují, bez ohledu na to, kolikrát se může ve vzorku vyskytnout.
Další námitka, kterou často slýchávám, je:„Zastaví se to někde náhodně a přehlédne skutečný problém ".To pochází z předchozí představy o tom, co je skutečným problémem. Klíčovou vlastností problémů s výkonem je, že odporují očekáváním. Vzorkování vám řekne, že něco je problém, a vaší první reakcí je nedůvěra. To je přirozené, ale můžete ujistěte se, že pokud zjistí problém, je skutečný a naopak.
Přidáno :Dovolte mi udělat Bayesovské vysvětlení, jak to funguje. Předpokládejme, že existuje nějaká instrukce I (volání nebo jinak), který je na zásobníku volání nějaký zlomek f času (a tedy stojí tolik). Pro zjednodušení předpokládejme, že nevíme co f je, ale předpokládejme, že je buď 0,1, 0,2, 0,3, ... 0,9, 1,0 a předchozí pravděpodobnost každé z těchto možností je 0,1, takže všechny tyto náklady jsou stejně pravděpodobné a-priori.
Pak předpokládejme, že vezmeme pouze 2 vzorky zásobníku a uvidíme instrukci I na obou vzorcích označeno pozorování o=2/2 . To nám dává nové odhady frekvence f z I , podle tohoto:
Prior
P(f=x) x P(o=2/2|f=x) P(o=2/2&&f=x) P(o=2/2&&f >= x) P(f >= x | o=2/2)
0.1 1 1 0.1 0.1 0.25974026
0.1 0.9 0.81 0.081 0.181 0.47012987
0.1 0.8 0.64 0.064 0.245 0.636363636
0.1 0.7 0.49 0.049 0.294 0.763636364
0.1 0.6 0.36 0.036 0.33 0.857142857
0.1 0.5 0.25 0.025 0.355 0.922077922
0.1 0.4 0.16 0.016 0.371 0.963636364
0.1 0.3 0.09 0.009 0.38 0.987012987
0.1 0.2 0.04 0.004 0.384 0.997402597
0.1 0.1 0.01 0.001 0.385 1
P(o=2/2) 0.385
Poslední sloupec říká, že například pravděpodobnost, že f>=0,5 je 92 %, což je nárůst oproti předchozímu předpokladu 60 %.
Předpokládejme, že předchozí předpoklady jsou odlišné. Předpokládejme, že předpokládáme P(f=0.1) je 0,991 (téměř jisté) a všechny ostatní možnosti jsou téměř nemožné (0,001). Jinými slovy, naše předchozí jistota je, že I je levný. Pak dostaneme:
Prior
P(f=x) x P(o=2/2|f=x) P(o=2/2&& f=x) P(o=2/2&&f >= x) P(f >= x | o=2/2)
0.001 1 1 0.001 0.001 0.072727273
0.001 0.9 0.81 0.00081 0.00181 0.131636364
0.001 0.8 0.64 0.00064 0.00245 0.178181818
0.001 0.7 0.49 0.00049 0.00294 0.213818182
0.001 0.6 0.36 0.00036 0.0033 0.24
0.001 0.5 0.25 0.00025 0.00355 0.258181818
0.001 0.4 0.16 0.00016 0.00371 0.269818182
0.001 0.3 0.09 0.00009 0.0038 0.276363636
0.001 0.2 0.04 0.00004 0.00384 0.279272727
0.991 0.1 0.01 0.00991 0.01375 1
P(o=2/2) 0.01375
Nyní to říká P(f >= 0.5) je 26 %, což je nárůst oproti předchozímu předpokladu 0,6 %. Bayes nám tedy umožňuje aktualizovat náš odhad pravděpodobných nákladů I . Pokud je množství dat malé, neřekne nám přesně, jaká je cena, pouze to, že je dostatečně velké, aby stálo za to opravit.
Ještě další způsob, jak se na to podívat, se nazývá pravidlo posloupnosti. Pokud dvakrát hodíte mincí a oběkrát se objeví hlava, co vám to říká o pravděpodobné váze mince? Respektovaným způsobem odpovědi je řekněme, že jde o distribuci Beta s průměrnou hodnotou (number of hits + 1) / (number of tries + 2) = (2+1)/(2+2) = 75% .
(Klíčem je, že vidíme I více než jednou. Pokud to vidíme jen jednou, kromě toho f nám to moc neřekne> 0.)
Takže i velmi malý počet vzorků nám může říct hodně o nákladech na instrukce, které vidí. (A uvidí je s frekvencí, která je v průměru úměrná jejich ceně. Pokud n jsou odebrány vzorky a f je cena, pak I se objeví na nf+/-sqrt(nf(1-f)) Vzorky. Příklad, n=10 , f=0.3 , to je 3+/-1.4 ukázky.)
Přidáno :Chcete-li poskytnout intuitivní pocit z rozdílu mezi měřením a náhodným vzorkováním zásobníku:
Nyní existují profilovači, kteří vzorkují zásobník, dokonce i v čase nástěnných hodin, ale co vyjde je měření (neboli hot path, neboli hot spot, před kterým se může „úzké hrdlo“ snadno schovat). Co vám neukážou (a snadno by mohli), jsou samotné vzorky. A pokud je vaším cílem najít počet z nich, které potřebujete vidět, je v průměru , 2 děleno zlomkem času, který to trvá. Pokud to tedy trvá 30 % času, ukáže to v průměru 2/,3 =6,7 vzorků a šance, že to ukáže 20 vzorků, je 99,2 %.
Zde je ukázka rozdílu mezi zkoumáním měření a zkoumáním vzorků zásobníku. Překážkou může být jedna velká skvrna, jako je tato, nebo mnoho malých, na tom nezáleží.
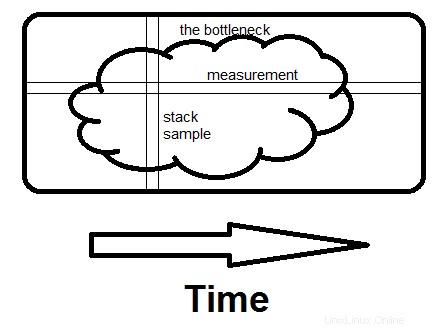
Měření je horizontální; říká vám, jaký zlomek času zabírají konkrétní rutiny. Vzorkování je vertikální. Pokud existuje nějaký způsob, jak se vyhnout tomu, co celý program v tu chvíli dělá, a pokud to vidíte na druhém vzorku , našli jste překážku. V tom je ten rozdíl – vidět celý důvod stráveného času, ne jen kolik.
Valgrind můžete použít s následujícími možnostmi
valgrind --tool=callgrind ./(Your binary)
Vygeneruje soubor s názvem callgrind.out.x . Poté můžete použít kcachegrind nástroj pro čtení tohoto souboru. Poskytne vám grafickou analýzu věcí s výsledky, jako například, které linky kolik stojí.
Předpokládám, že používáte GCC. Standardní řešení by bylo profilovat pomocí gprof.
Nezapomeňte přidat -pg ke kompilaci před profilováním:
cc -o myprog myprog.c utils.c -g -pg
Ještě jsem to nezkoušel, ale slyšel jsem dobré věci o google-perftools. Rozhodně to stojí za vyzkoušení.
Související otázka zde.
Několik dalších buzzwords, pokud gprof nedělá práci za vás:Valgrind, Intel VTune, Sun DTrace.