Úvod
Počítačová technika je nezbytnou součástí vědeckého výzkumu. Matematické, inženýrské, vědecké a další technické problémy jsou složité a vyžadují výpočetní výkon a rychlost. Python poskytuje knihovnu SciPy pro výpočetní řešení technických problémů.
Tento článek představuje výukový program SciPy a jak implementovat kód v Pythonu s příklady.

Předpoklady
- Nainstalovaný Python 2.7 nebo Python 3
- Prostředí Python pro spouštění kódu.
- Nainstalována knihovna SciPy.
- Nainstalována knihovna NumPy (postupujte podle našeho průvodce:Jak nainstalovat NumPy).
- Nainstalovaná knihovna Matplotlib pro vykreslování (volitelné).
Co je SciPy?
SciPy (Sci entific Py thon) je open-source vědecký výpočetní modul pro Python. Na základě NumPy obsahuje SciPy nástroje pro řešení vědeckých problémů. Vědci vytvořili tuto knihovnu, aby reagovala na jejich rostoucí potřeby při řešení složitých problémů.
SciPy vs NumPy
Knihovna NumPy (Num erical Py thon) provádí numerické výpočty. Vědci používají tuto knihovnu pro práci s poli, protože NumPy pokrývá základní použití v datové vědě, statistice a matematice.
SciPy pokrývá pokročilé výpočty a funkce. Tato knihovna přidává další funkce datové vědy, všechny funkce lineární algebry a standardní vědecké algoritmy.
Proč používat SciPy?
Knihovna SciPy staví na NumPy a funguje na polích. Výpočetní výkon je rychlý, protože NumPy používá C pro vyhodnocení.
Vědecký zásobník Pythonu je podobný jako MATLAB, Octave, Scilab a Fortran. Hlavním rozdílem je, že Python se snadno učí a píše.
Podbalíčky SciPy
Knihovna SciPy má různé skupiny dílčích balíčků. Existují dva způsoby, jak importovat dílčí balíčky z modulu SciPy:
import scipy.<sub package name> as <alias>Nebo alternativně:
from scipy import <sub package name> as <alias>V obou způsobech importu je alias volitelný.
Funkce SciPy
SciPy obsahuje mnoho funkcí primárního pole dostupných v NumPy a některé běžně používané moduly z dílčích balíčků SciPy.
Chcete-li importovat funkci z dílčího balíčku, použijte:
from scipy.<subpackage> import <function>Základní funkce
Chcete-li získat nápovědu a informace pro jakoukoli funkci SciPy, použijte help() příkaz:
help(<name of function>)
help() příkaz nepotřebuje parametry. Po provedení bez parametrů se zobrazí výzva, kde zadáte název funkce.
Dalším rychlým způsobem, jak získat pomoc s jakýmkoli příkazem v Pythonu, je napsat název příkazu, dát na konec otazník a spustit kód.
Speciální funkce
Speciální funkce v modulu SciPy zahrnují běžně používané výpočty a algoritmy. Všechny speciální funkce přijímají pole NumPy jako vstup. Výpočty jsou založeny na prvcích.
Chcete-li importovat special dílčí balíček, použijte:
import scipy.special as specialNebo alternativně:
from scipy import special
Chcete-li importovat konkrétní funkci ze special dílčí balíček, použijte:
from scipy.special import <function name>Faktoriální
Vyhodnoťte faktoriál libovolného čísla spuštěním:
special.factorial(<integer or array>)Chcete-li například najít faktoriál deseti, použijte:
special.factorial(10)
Permutace a kombinace
Chcete-li zjistit počet permutací, použijte:
special.perm(<number of elements>, <number of elements taken>)Chcete-li například zobrazit počet permutací tří prvků provedených po dvou:
special.perm(6,2)
Podobně najděte počet kombinací pomocí:
special.comb(<number of elements>, <number of elements taken>, repetition=<True or False>)Chcete-li zjistit počet kombinací tří prvků braných po dvou s opakováním, zadejte:
special.comb(6,2, repetition=True)
Permutace a kombinace se používají v algoritmech třídění počítačových věd.
Exponenciální funkce
Exponenciální funkce vyhodnocují exponenty pro různé základy.
Vypočítejte exponenty základu deset pomocí:
special.exp10(<integer or array>)Například:
special.exp10([0,1,2])
Informatika často používá exponenciální funkce základu dva:
special.exp2(<integer or array>)Vypočítejte desátou mocninu základu dva pomocí:
special.exp2(10)
Logaritmický součet exponenciál
Logaritmický součet exponenciál (LSE nebo LogSumExp) je aproximace používaná algoritmy strojového učení. Vypočítejte LSE pomocí:
special.logsumexp(<integer or array>)
Besselova funkce
Besselovy funkce se objevují při šíření vln, zpracování signálu a problémech se statickým potenciálem. Najděte Besselovu funkci prvního druhu pomocí:
special.jn(<integer order>, <integer or array>)Využijte celý zásobník k vizualizaci Besselovy funkce. Chcete-li najít Besselovu funkci druhého řádu prvního druhu, použijte:
#import stack
import scipy.special as special
import matplotlib.pyplot as plt
import numpy as np
#The X-axis
x = np.linspace(1,50,100)
#Bessel function of the first kind order two
jn1 = special.jn(2,x)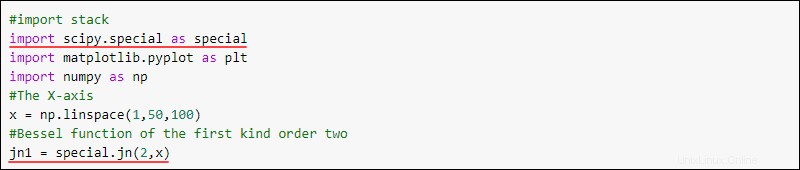
Vykreslete výsledky:
#Plotting
plt.title('Bessel function first kind order two')
plt.plot(x, jn1)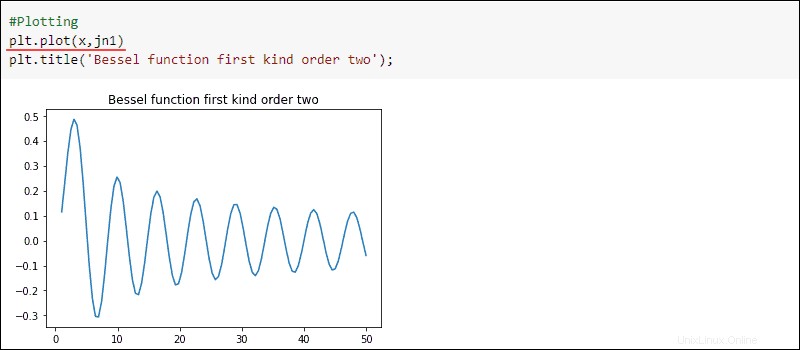
Integrace a funkce ODE
SciPy poskytuje dílčí balíček pro výpočty s určitými integrály. Chcete-li importovat integrate dílčí balíček, použijte:
import scipy.integrate as integrateNebo alternativně:
from scipy import integrate
Importujte konkrétní funkci z dílčího balíčku integrate s:
from scipy.integrate import <function name>Obecná integrace
Vypočítejte integrál jedné proměnné s quad funkce z integrate dílčí balíček:
integrate.quad(<function>, <lower limit>, <upper limit>)
function vstup je definován pomocí funkce lambda.
Například pro výpočet určitého integrálu funkce x+1 mezi nulou a jedničkou:
from scipy import integrate
f = lambda x: x+1
integrate.quad(f, 0, 1)Výstup ukazuje dvě hodnoty. První hodnota je vyhodnocený integrál a druhá je chyba odhadu.

Funkce optimalizace
SciPy má optimalizační podbalíček pro nalezení minima nebo maxima funkce. optimize dílčí balíček obsahuje řešiče a algoritmy pro nalezení lokálních a globálních optimálních hodnot.
Import dílčího balíčku Optimalizace:
from scipy import optimizeNebo použijte:
import scipy.optimize as optimize
Chcete-li importovat konkrétní funkci z dílčího balíčku optimize , spustit:
from scipy.optimize import <function name>Minimalizujte funkci
Nalezení minima funkce se používá ve strojovém učení ke snížení ztrát (nebo chyb) algoritmu.
Můžete například vytvořit funkci a najít minimum. Chcete-li to provést, použijte fmin funkce z optimize dílčí balíček ve SciPy:
#Import stack
import numpy as np
from scipy import optimize
#Defining inverse sine function
def f(x):
return -np.sin(x)
#X-axis
x = np.linspace(0,5,100)
#Starting point
start = 3
#Simplex algorithm for optimization
optimized = optimize.fmin(f,start)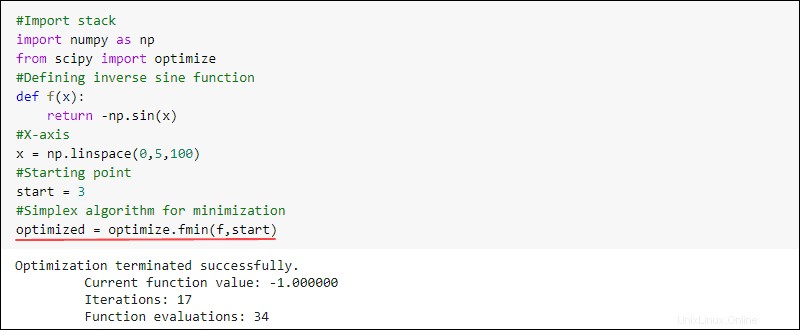
Chcete-li vykreslit výsledek, spusťte:
import matplotlib.pyplot as plt
plt.plot(x, f(x))
plt.scatter(start,f(start))
plt.scatter(optimized, f(optimized))
plt.legend(['Function -sin(x)', 'Starting point', 'Optimized minimum'])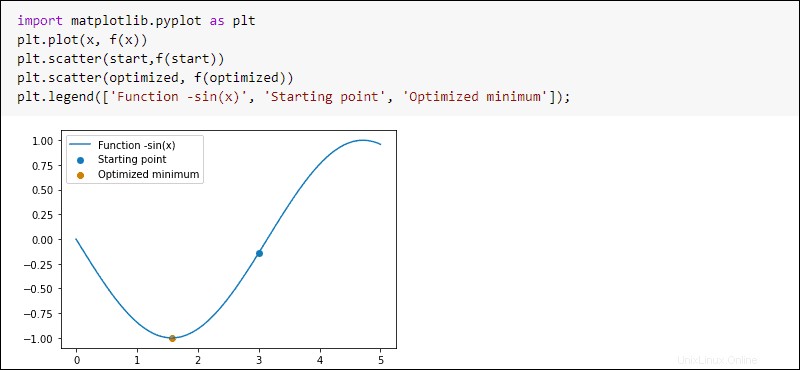
Furierovy transformační funkce
SciPy obsahuje dílčí balíček pro funkce Fourierovy transformace nazvaný fftpack . Transformace jsou diskrétní Fourierovy transformace (DFT). Všechny transformace jsou aplikovány pomocí algoritmu Fast Fourier Transformation (FFT).
Chcete-li importovat fftpack dílčí balíček, použijte:
import scipy.fftpack as fftpackNebo:
from scipy import fftpackRychlá Fourierova transformace
Jako příklad vytvořte periodickou funkci jako součet tří sinusových vln:
import numpy as np
freq_samp = 100
#Time
t = np.linspace(0, 1, freq_samp*2, endpoint = False )
#Frequencies
f1, f2, f3 = 1, 5, 20
#Amplitudes
A1, A2, A3 = 3, 2, 1
x1 = A1*np.sin(f1*2*np.pi*t)
x2 = A2*np.sin(f2*2*np.pi*t)
x3 = A3*np.sin(f3*2*np.pi*t)
#Sum of waves
x = x1+x2+x3
Vykreslete vlny pomocí matplotlib :
import matplotlib.pyplot as plt
plt.subplot(2,1,1)
plt.plot(t,x1,t,x2,t,x3)
plt.subplot(2,1,2)
plt.plot(t,x)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude');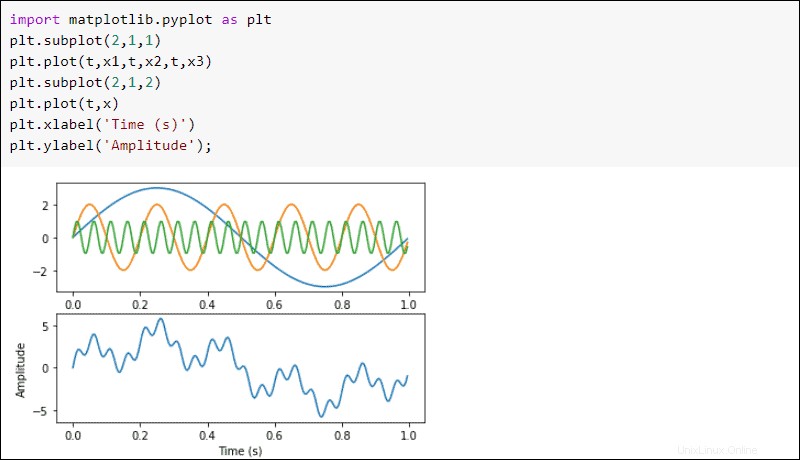
Dále použijte fft a fftfreq funkce z fftpack k provedení Fourierovy transformace signálu.
from scipy import fftpack
A = fftpack.fft(x)
freq = fftpack.fftfreq(len(x))*freq_samp*2
Vykreslete výsledky, abyste viděli frekvenční doménu:
plt.stem(freq,np.abs(A)/freq_samp,use_line_collection=True)
plt.xlim(-25,25)
plt.xlabel('Frequency (Hz)')
plt.ylabel('Amplitude')
plt.grid()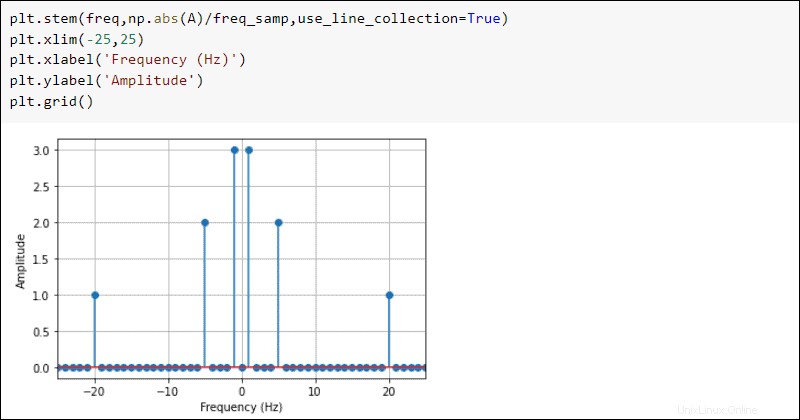
Funkce zpracování signálu
Dílčí balíček signal zahrnuje funkce používané při zpracování signálu. Chcete-li importovat signal , spustit:
import scipy.signal as signalNebo alternativně:
from scipy import signalKonvoluce
Běžným úkolem při zpracování signálu je konvoluce. Podbalíček SciPy signal má funkci convolve k provedení tohoto úkolu. Například vytvořte dva signály s různými frekvencemi:
import numpy as np
#Time
t = np.linspace(0,1,100)
#Frequency
f1, f2 = 5, 2
#Two signals of different frequencies
first_signal = np.sin(f1*2*np.pi*t)
second_signal = np.sin(f2*2*np.pi*t)
Vykreslete signály:
import matplotlib.pyplot as plt
#Plotting both signals
plt.subplot(2,1,1)
plt.plot(t, first_signal)
plt.subplot(2,1,2)
plt.plot(t, second_signal)
plt.ylabel('Amplitude')
plt.xlabel('Time (s)')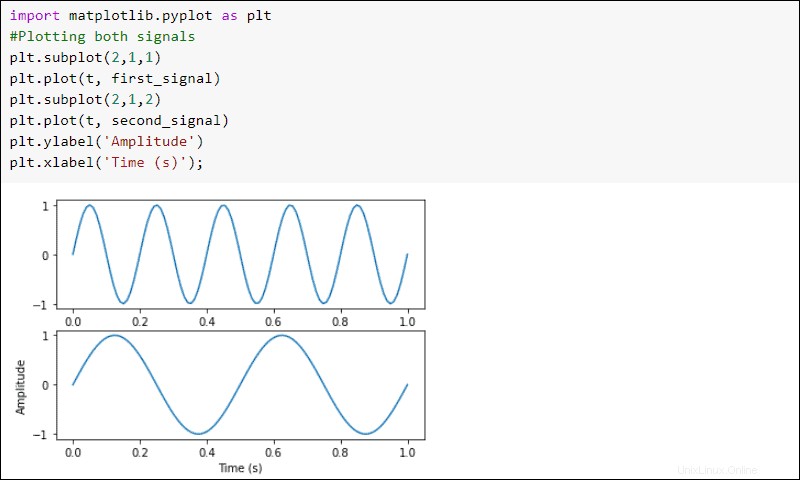
Importujte signal dílčí balíček z scipy . Použijte convolve funkce ze signal dílčího balíčku ke spojení dvou signálů:
#Importing the signal subpackage
from scipy import signal
#Convolving two signals
convolution = signal.convolve(first_signal, second_signal, mode='same')
Vykreslete výsledky:
#Plotting the result
plt.plot(t, convolution)
plt.xlabel('Time (s)')
plt.ylabel('Amplitude')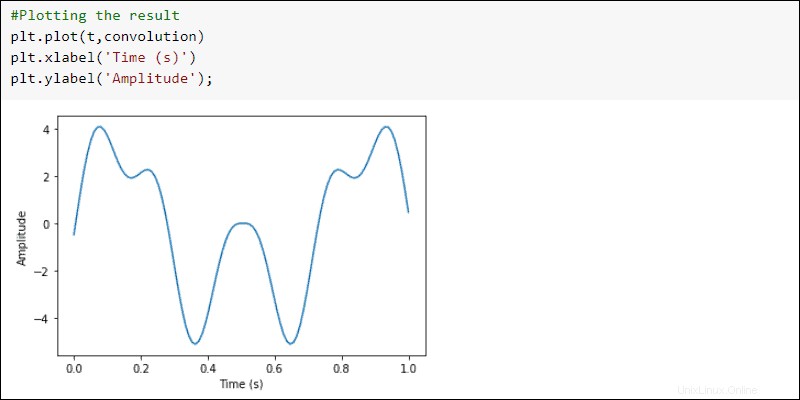
Funkce interpolace
Interpolace se používá v oblasti numerické analýzy ke zobecnění hodnot mezi dvěma body. SciPy má interpolate podbalíček s interpolačními funkcemi a algoritmy.
Importujte interpolate dílčí balíček s:
import scipy.interpolate as interpolateNebo:
from scipy import interpolateJednorozměrná interpolace
SciPy interpolate dílčí balíček má interp1d funkce pro jednorozměrnou interpolaci dat. Jako příklad vytvořte hračku data pomocí numpy :
import numpy as np
#Create toy data
x = np.arange(0,10,0.5)
y = np.sin(x)
Interpolujte data pomocí interp1d z interpolate dílčí balíček:
from scipy import interpolate
#Interpolate
f = interpolate.interp1d(x, y)
#Create interpolation function
x_i = np.arange(0,10,3)
y_i = f(x_i)
Vykreslete výsledky:
#Plot results
plt.scatter(x,y)
plt.plot(x_i, y_i)
plt.legend(['Interpolation', 'Data points'])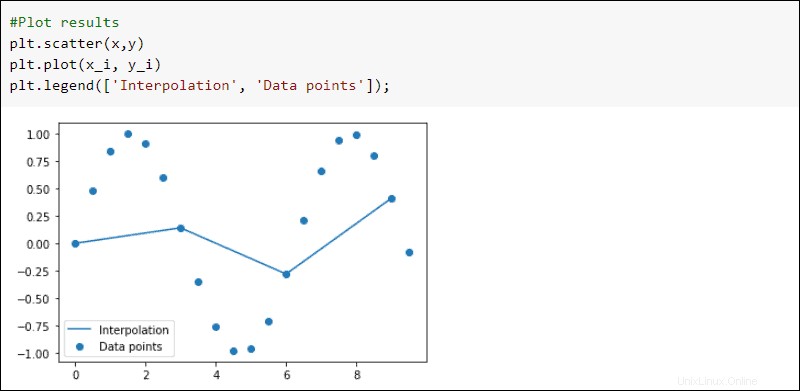
Lineární algebra
SciPy má plně vybavený dílčí balíček lineární algebry. Podbalíček lineární algebry SciPy je optimalizován pomocí knihoven ATLAS LAPACK a BLAS pro rychlejší výpočty.
Chcete-li importovat balíček lineární algebry ze SciPy, spusťte:
import scipy.linalg as linalgNebo použijte:
from scipy import linalgVšechny funkce lineární algebry očekávají pro vstup pole NumPy.
Rozhodující
Vypočítejte determinant matice pomocí det z linalg dílčí balíček:
linalg.det(<numpy array>)Například:
import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the determinant
linalg.det(A)
Inverzní matice
Určete inverzní matici pomocí inv :
linalg.inv(<numpy array>)Například:
import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3,4]])
from scipy import linalg
#Calculate the inverse matrix
linalg.inv(A)
Vlastní vektory a vlastní hodnoty
Vlastní vektory a vlastní čísla jsou metodou rozkladu matice. Problém vlastní hodnota-vlastní vektor je běžně implementovaný problém lineární algebry.
eig funkce najde vlastní čísla a vlastní vektory matice:
linalg.eig(<numpy array>)Výstup vrací dvě pole. První obsahuje vlastní čísla a druhý vlastní vektory pro danou matici. Například:
import numpy as np
#Generate a 2D array
A = np.array([[1,2],[3, 4]])
from scipy import linalg
#Calculate the eigenvalues and eigenvectors
linalg.eig(A)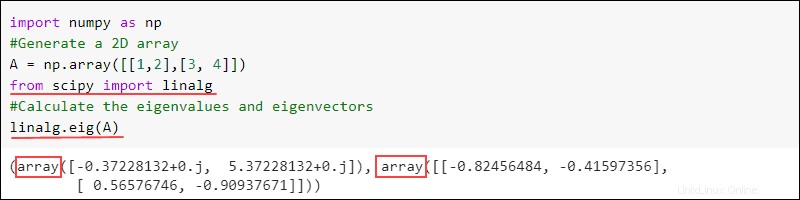
Struktury a algoritmy prostorových dat
Struktury prostorových dat jsou objekty složené z bodů, čar a povrchů. SciPy má algoritmy pro prostorové datové struktury, protože se vztahují na mnoho vědeckých disciplín.
Importujte spatial dílčí balíček od SciPy s:
import scipy.spatial as spatialNebo:
from scipy import spatialPozoruhodným příkladem prostorového algoritmu je Voronoiův diagram. Pro danou sadu bodů Voronoiovy mapy rozdělují rovinu na oblasti. Pokud nový bod spadá do oblasti, je bod v oblasti nejbližší soused.
Jako příklad vytvořte Voronoiův diagram z dvaceti náhodných bodů:
from scipy.spatial import Voronoi
import numpy as np
points = np.random.rand(20,2)
voronoi = Voronoi(points)
from scipy.spatial import voronoi_plot_2d
fig = voronoi_plot_2d(voronoi,show_vertices=False)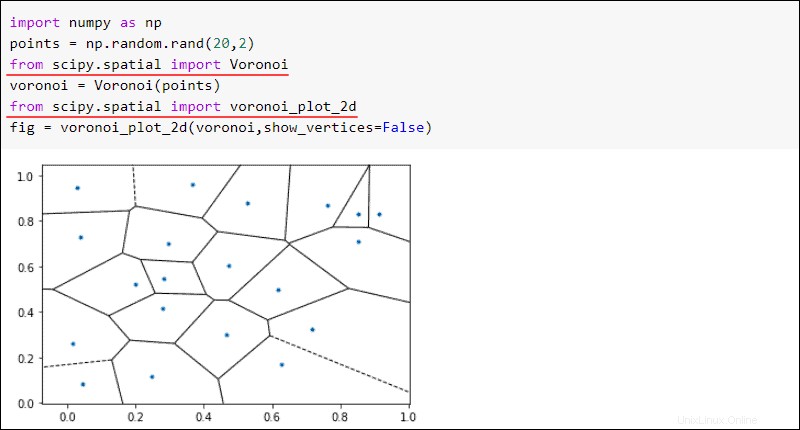
Zpracování obrázků
SciPy má dílčí balíček pro různé n-rozměrné zpracování obrazu. Chcete-li importovat ndimage dílčí balíček, spusťte:
import scipy.ndimage as ndimageNebo použijte:
from scipy import ndimage
SciPy misc dílčí balíček obsahuje ukázkový obrázek pro demonstrační účely. Chcete-li importovat misc dílčí balíček a ukažte obrázek:
from scipy import misc
from matplotlib import pyplot as plt
raccoon = misc.face()
#show image
plt.imshow(raccoon)
plt.show()
Importujte ndimage dílčího balíčku a použijte uniform_filter k obrazu. Ukažte obrázek, abyste viděli výsledky:
from scipy import ndimage
filtered = ndimage.uniform_filter(raccoon)
plt.imshow(filtered)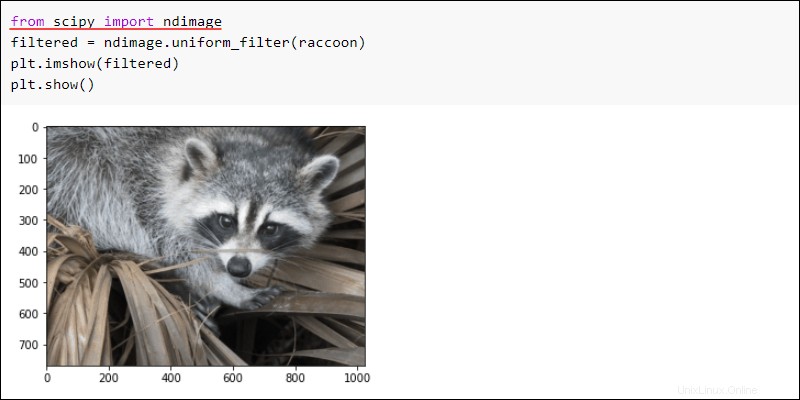
File IO (File Input / Output Package)
SciPy má souborový vstupní a výstupní dílčí balíček nazvaný io . io subpackage se používá pro čtení a zápis datových formátů z různých vědeckých výpočetních programů a jazyků, jako je Fortran, MATLAB, IDL atd.
Importujte soubor io dílčí balíček od SciPy s:
import scipy.io as sioNebo použijte:
from scipy import io as sio